Dissonance, Mahler, and Beyond - Part 1
Hello! I’m Ste, and I’m researching voice AI at Gaudio Lab.
Lately, I’ve been diving into the music of the classical composer Gustav Mahler here at Gaudio Lab!
Mahler is known for his music, which is full of strong dissonances and intricate structures.
To express the emotions of love and pain he felt throughout his life, he used dissonance as a key element in his compositions. Let’s explore these dissonances from an acoustical, musical, and historical perspective!
1 Dissonance
Music is an art that uses sound as its material. Just like how meat or seafood is essential to make a flavorful soup, harmonious chords are the base of music. But, just like those basic ingredients alone can’t make a rich soup, the addition of dissonance, with its strong personality, is what gives music its depth and variety. A piece of music made only from harmonious tones would sound monotonous, like a simple broth made only from meat. Dissonance, on the other hand, can provide stimulation and create tension, making the music more compelling—like adding seasoning to a dish.
1.1 Complex Integer Ratios
How does dissonance occur? It has to do with the ratio of frequencies between two notes. Sound is created by vibrating objects, and when two notes vibrate at a simple integer ratio, we hear them as consonant. But when the ratio between their frequencies is more complex, we hear them as dissonant. Here’s a table showing the ratios and consonance/dissonance of different intervals based on the note A:
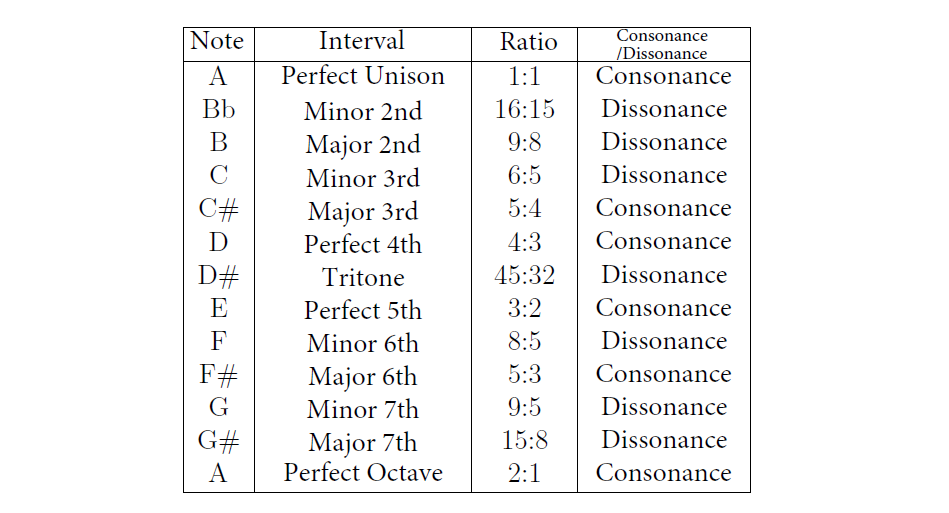
For example, the perfect octave (2:1 ratio) and the perfect fifth (3:2 ratio) sound harmonious to the ear. These ratios form the foundation of basic harmony. As the frequency ratio becomes more complex, dissonance emerges. For example, intervals like the minor second (16:15) and the augmented fourth (45:32) sound dissonant. These dissonances are useful in music to express tension or emotional shifts. But what happens when the ratio is extremely complex, like 441:440, where the two notes’ frequencies differ only slightly?
1.2 Beating
Another way to understand dissonance is through a phenomenon called "beating." This occurs when two frequencies that are very close to each other vibrate together, causing their amplitudes to modulate periodically. If this modulation happens quickly, it can create an unpleasant tension—almost like a drum being struck rapidly. This effect is called "beating." According to the physicist Helmholtz, the tension caused by beating is most noticeable in the 30-40Hz range. [2] The principle behind beating is simple, and can be derived from the addition formula of trigonometric functions.
If we combine two sine waves with frequencies f1 and f2, the resulting wave can be expressed as:
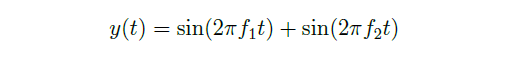
Using the trigonometric addition formula, we get:
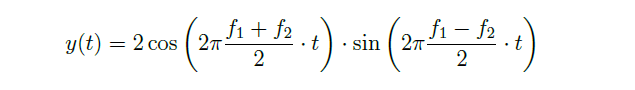
The cosine term represents the center frequency, vibrating at (f1+f2)/2, while the sine term represents the beating frequency, vibrating at |f1−f2|/2. This is fascinating: when we combine two waves with different frequencies, a new center frequency appears, and amplitude modulation happens, causing the sound to either amplify or dampen. I remember when I was younger, I thought that when I played C and E on the piano, I would hear the note D in between, but I was confused when this didn’t happen. It’s amazing to think that this phenomenon happens when the sound sources are the same and frequency differences are so small!
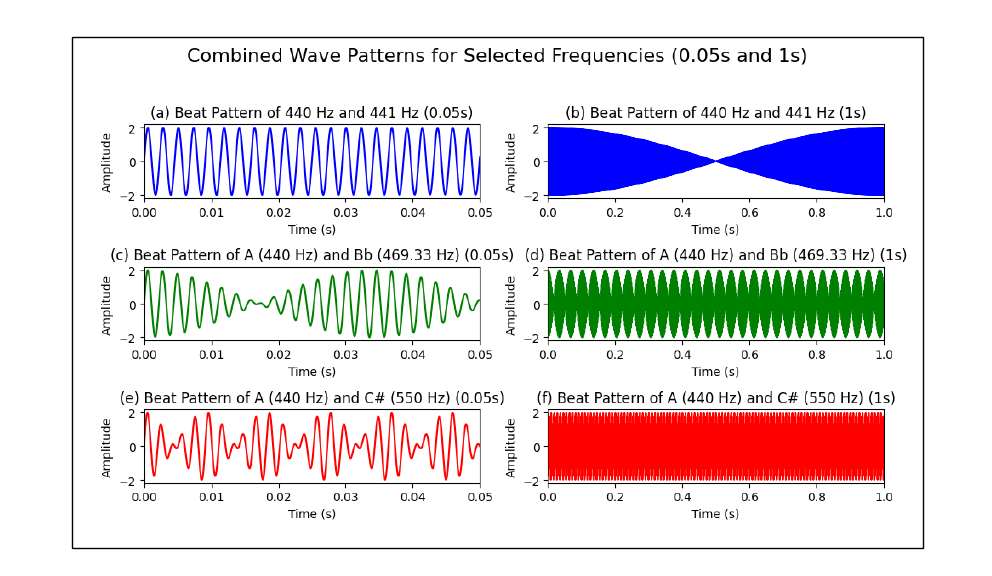
Figure 1 shows the result of combining two different frequencies in a graph. (a) and (b) show the combination of 440Hz and 441Hz. Despite the complex ratio, this combination sounds consonant, with a center frequency of (440+441)/2 = 440.5Hz and a beating frequency of (441−440)/2 = 0.5Hz. This results in a slow modulation, producing a "waa-waa" effect without creating the percussion-like tension we associate with dissonance.
(c) and (d) show a dissonant minor second, with a beating frequency of 29.33Hz. This rapid beating creates tension, like a drum being struck about 30 times per second, which makes the sound dissonant. (e) and (f) show consonant tones of A and C#, with a beating frequency of 110Hz. This frequency is too fast for us to perceive as rhythm, so we hear the notes as independent and consonant.
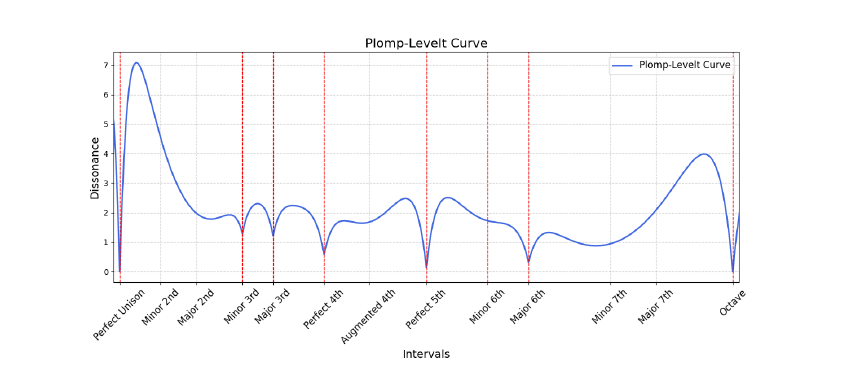
[2] Helmholtz suggested this analysis of dissonance through beating, and [3] Plomp and Levelt, after experimenting with human subjects, created a graph of how different ratios within an octave affect the perception of dissonance. If we reproduce this graph based on intervals, we get Figure 2. From the graph, we can see that intervals like the perfect unison, major/minor thirds, perfect fourth, perfect fifth, and major/minor sixth have low dissonance compared to neighboring intervals. The dissonance increases between the minor second and perfect unison due to the tension created by beating. However, as the interval nears a perfect unison, the dissonance quickly decreases because the beating frequency slows down, no longer creating that percussive tension.
1.3 Non-Chord Tones
As mentioned earlier, dissonance is essential to music because it adds variety and depth. In music, the relationship between intervals becomes more structured, forming a hierarchy of harmonic tones that make up the system of harmony. For example, the C-E-G chord forms the harmony of the C major chord. The G note, a perfect fifth above C, is consonant, and the E note, also relatively consonant, fits in between. Once this harmony is established, all other notes, like D, F, A, and B, are considered non-chord tones, as they create dissonances with C, E, or G.
One of the key features of classical music, such as Mozart’s, is the clear hierarchy between chord tones and non-chord tones. Non-chord tones create tension with the other chord tones, and this
tension is resolved when non-chord tones move to a chord tone. This process is known as "resolution" in musical terms. Within a clear harmonic structure, this tension-resolution pattern moves the music forward, like fitting pieces of a puzzle together. It’s similar to how in language, nouns are modified by adjectives and verbs, and adjectives and verbs are further modified by adverbs. Music without non-chord tones, consisting only of harmony, might sound innocent and naive, like a child speaking only in nouns, without adjectives or verbs.

Figure 3 shows how Mozart creates dissonance in his string quartet and elegantly resolves it. The passage begins with the cello playing C notes in succession. After two beats, the viola introduces an Ab note, creating a sense of tension due to the use of a first inversion chord. Normally, music starts with a root-position chord, and we expect the perfect fifth to be present. Soon, the second violin adds an Eb, forming an Ab chord and slightly alleviating the tension.
However, this is quickly undone by the A♮ played by the first violin on the next beat. Even though the viola moves to a G note to soften the dissonance, the G note continues to create discomfort, as it forms a major second interval with the A♮. Additionally, the Eb from the second violin, which was aligned with the Ab major chord, now forms an augmented fourth when paired with the A♮, creating the dissonance known as the "devil's interval." Eventually, the viola’s A resolves to F#, and the second violin’s Eb resolves to D, completing the resolution.
In this work, Mozart uses counterpoint, inherited from 16th-century church music, to carefully manage intervals, skillfully moving between consonance and dissonance. However, he stays within the limits of classical harmony and counterpoint, experimenting only within the boundaries of traditional tonality, leaving the development of functional harmony to his successors.
Dissonance, Mahler, and Beyond – Part 2 to follow
References
[1] Jens Malte Fischer. Gustav Mahler. Yale University Press, 2011.
[2] Hermann LF Helmholtz. On the Sensations of Tone as a Physiological Basis for the Theory of Music. Cambridge University Press, 2009.
[3] Reinier Plompand Willem JM Levelt. “Tonal consonance and critical bandwidth”. In: Journal of the Acoustical Society of America38(1965), pp. 548–560.


